ALL ABOUT THE DATA: Decisions throughout the acquisition process are informed by data collected from many sources. Often, test are designed to help us understand how changes in the inputs will affect some response, the end result that is being measured. (Image by Getty Images)
Acquisition decisions are inherently risky; we must learn to manage risk like a successful gambler.
by Jason Martin
Much like a high-stakes gambler deciding whether to raise, check or fold, the acquisition process for military systems is a series of high-stakes decisions in which we commit more resources for further development (raise) or stop funding an effort (fold). There is seldom an option to delay a decision with no cost (check). Ultimately, Soldiers’ lives are at stake. Successful gamblers understand the risks they are taking and know how to consider these risks when making decisions.
Acquisition leaders emphasize that the Army needs to accept more risk when making decisions, and, for acquisition professionals, comfort with risk comes from understanding it. Understanding risk allows us to make appropriately risk-aware decisions as individuals and as an organization. We must make decisions the way successful gamblers do—with a clear understanding of risk. Throughout the acquisition process, how can decision-makers best understand the risks they are taking and make risk-aware decisions? What kind of information must decision-makers insist on being provided?
To manage risk when making a decision, Army acquisition professionals often collect data through testing or experimentation (for the rest of the article, simply called testing). We then analyze the data to create the information needed to support the decision. The cost of collecting data often limits the data we can collect; therefore, there are limitations in what we can learn from the data. For example, when testing $500,000 missiles, the costs of missiles, test range time and personnel can quickly become too great, so the number of missiles that can be tested is limited. When data is analyzed appropriately, an important way the data limitations will show up is in the form of uncertainty in our conclusions. Understanding this helps us make risk-aware decisions.
We collect data for many purposes and from many sources to inform decisions throughout the acquisition process. Examples include performing basic science experiments to identify technologies worthy of further investment, running computer models to determine the best design characteristics, using flight simulators to assess pilot-vehicle interfaces and range testing to support vendor selection or a fielding decision. In many cases, we test to understand how changes in the inputs to a process affect some response, the end result that is being measured. Though the example below is of a fielding decision, the points made in this article apply any time we attempt to understand how inputs affect a response.

A PRICEY TEST: Collecting data comes with a cost. If the cost is too high, that may limit the quantity of data being collected, which in turn limits what can be learned from the data in question. For a test involving $500,000 missiles, the costs would mount quickly and testing would likely be limited. (Photo by Jason Cutshaw, U.S. Army Space and Missile Defense Command)
A RISKY BET?
Consider a system that warns aircraft pilots of incoming missiles. A program manager (PM) must decide whether to field a new version of software or continue with the current version.
In this simple case there is only one input, the software version (current or new), but there could be many more. To determine whether the new software is “better” and should be fielded, the response being measured is whether the system successfully detects a simulated missile (success or failure). The PM will consider the new software worthy of fielding if its probability of successfully detecting a missile is at least 5 percent greater than for the current software. The PM has budgeted 20 test events for each software version.
During the test, the new software is successful in 18 of 20 events (90 percent success rate), and the current software is successful in 16 of 20 events (80 percent success rate). How should the PM decide whether to field the new software? One common approach is to select the software with the greater success rate—in this case the new software. But is this a good decision? Although the new software performed 10 percent better, do test results provide sufficient evidence that the new software really is better? Is it possible to get these results even if the new software is equivalent or even worse? If so, how likely is that to happen? To make a risk-aware decision, the PM must be able to answer these questions. Otherwise, the PM is acting like an unskilled gambler. These questions and others can be answered using appropriate statistical analysis methods.
The plot in the figure below is a result of statistical analysis of the test data described above (more specifically, logistic regression was used for analysis). Understanding what the plot tells us is critical to making a risk-aware decision.
Notice that the peak of the distribution is very close to 10 percent and is designated by the black dot at the bottom of the distribution. This represents our best estimate of the improvement when using the new software, and should not be a surprise since the new software had a 10 percent greater success rate during testing.
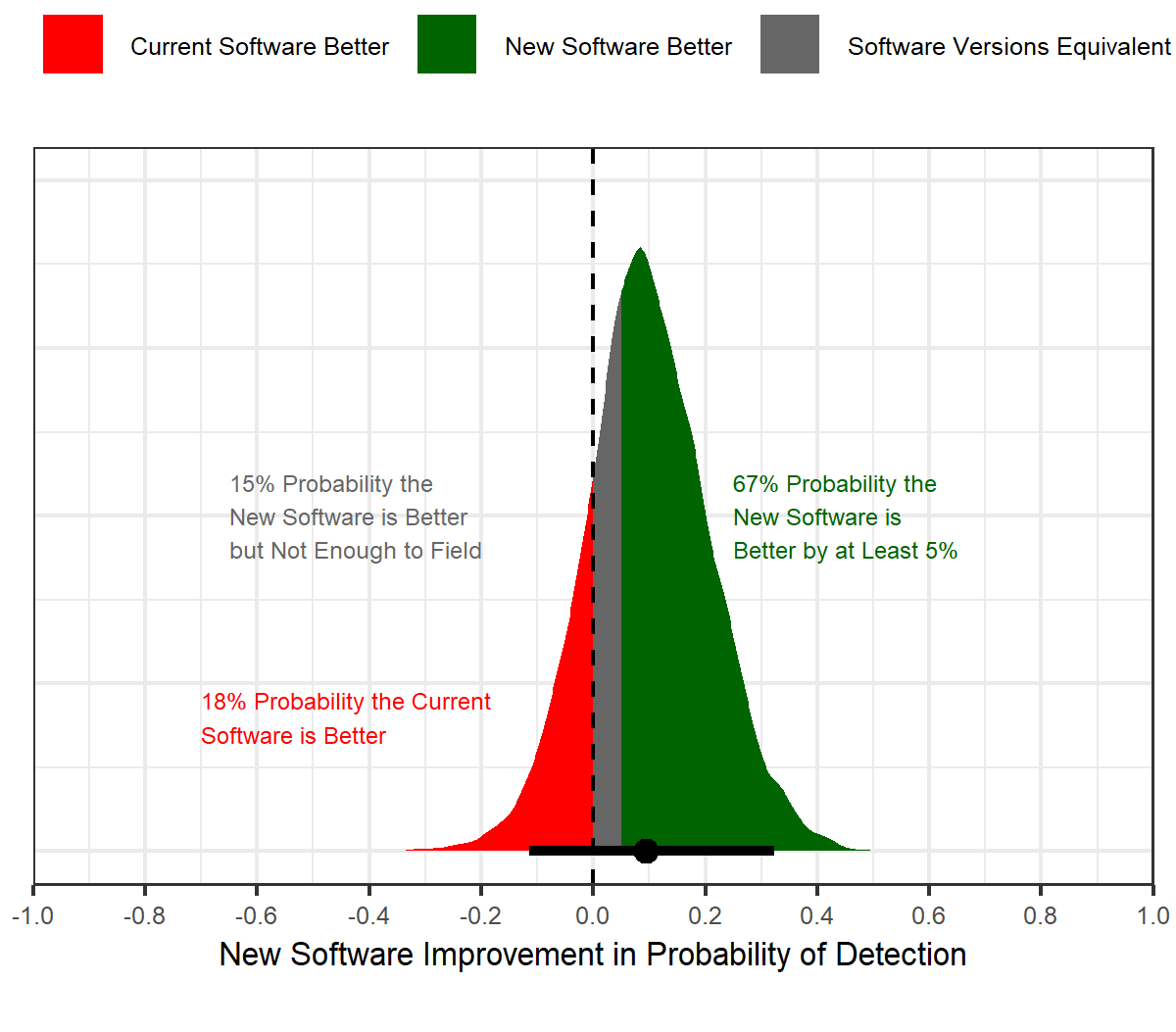
PROBABLE CAUSE: Statistical analysis of the test data yields this result, which demonstrates the probability of detection. Understanding the meaning of the data is critical to making a risk-aware decision. (Image by the author)
However, because we have limited data, there is uncertainty about the true improvement that the new software would provide in the many events that would occur over the lifetime of a fielded system.
This uncertainty is represented by the black line at the bottom of the distribution, which indicates the range of values 95 percent likely to contain the actual (and unknown) improvement. The line ranges from -0.07 to 0.28, and this tells us it is reasonable to conclude the new software results in an improvement of -7 percent (the new software is 7 percent less likely to detect a missile, and is inferior) to 28 percent (the new software is 28 percent more likely to detect a missile, and is better). Although the PM would prefer a definitive answer to the question “Is the new software better?”, it isn’t possible with the data available. To make a risk-aware decision, the PM must recognize this when deciding what to do.
The colored regions help us understand the risk we’re taking when making a decision. The green area contains 67 percent of the area in the distribution, and this tells us there is a 67 percent chance that the new software is better than the current software. We can also see that there is a 15 percent chance the two versions are equivalent (new software better but by less than 5 percent per the PM), and an 18 percent chance that the new software is actually worse in spite of the fact that it performed better in testing.
By understanding the information described above, the PM can make a risk-aware fielding decision by weighing the potential for fielding a better software against the risk of spending resources to field equivalent or inferior software. At a high level, there are three options:
- Field the new software with a 67 percent chance that it improves probability of detection by at least 5 percent and some potential for at least 28 percent improvement. The risk is that the PM will spend possibly substantial resources to field the software while accepting a 33 percent chance that Soldiers are receiving software that either degrades or does not sufficiently improve performance.
- Continue with the currently fielded software, save the cost of fielding and accept a 67 percent risk that Soldiers are not receiving improved software.
- Spend time and other resources to collect more data to more accurately understand the actual improvement provided by the new software.
The actual decision the PM would make could also depend on other factors and isn’t important for now. The point is that by quantifying the risk of fielding an inferior system or failing to field an improvement, the PM can weigh these risks against the cost of fielding, the cost of collecting additional data and other factors. The PM can also clearly communicate these risks to other stakeholders so that everyone understands the risks being taken. It is important to note that a common understanding of risk can significantly improve the ability of an organization to be more risk aware. This includes enabling an organization to constructively learn from failures instead of punishing them.
The example above shows one of many ways statistical analysis can be used to communicate uncertainty and risk. Using statistical analysis to quantify and understand risk clearly allows for a more risk-aware decision than simply choosing the new software because it had a 10 percent greater success rate during testing. While truly understanding risk can make a decision more difficult (even gut-wrenching), we owe it to our Soldiers to understand the risks involved when making decisions that affect them.
NOT ALL DATA IS CREATED EQUAL
While the focus of this article is on the importance of considering risk when making a decision, it is necessary to note the importance of the way we determine how much and what specific data to collect.
In the example above, the test included 20 events for each software version because that is what the PM had budgeted. This number of events arguably resulted in more risk than the PM desired when making the fielding decision. Budgeting for testing is frequently done by looking at what has been done in the past, just doing what seems reasonable or affordable, or arguing to further reduce testing until someone refuses. By leveraging system expert knowledge, statistical methods known as design of experiments allow us to control the uncertainty we expect in our conclusions even before resources are spent to execute a test.
These methods help us to manage risk and resources by allowing us to rigorously trade among the cost of a test, the amount of information we gain from a test, and the accuracy that we can achieve when doing statistical analysis on data.

A GAMBLER’S APPROACH: We should take a cue from successful gamblers, who make decisions with a clear understanding of the risks involved, rather than attempting to avoid risk entirely. (Image by Getty Images/Simon Webb and Duncan Nicholls)
In short, using design of experiments to plan tests allows us to use expert assumptions to determine a sufficient but not excessive number of test events to achieve acceptable levels of risk. In those situations where resources prevent us from limiting risk as much as desired, we can at least understand the risks we’re taking before resources are committed. Though used for decades by some to very successfully understand complex military systems, widespread use of design of experiments and statistical analysis across the DOD in all phases of research, development and fielding would provide substantial benefits. Methods and software tools are available that allow us to collect data and perform analysis to answer questions about even our most complex military systems.
CONCLUSION
Taking risks that ultimately impact the effectiveness and safety of our Soldiers is inherent in the acquisition process. By using design of experiments to plan tests and statistical methods to analyze the resulting data, we can most efficiently utilize resources to provide decision makers with a true understanding of risk. The costs of continuing to fund an effort (e.g. a specific research effort, system upgrade or program) can be substantial in terms of time and taxpayer dollars; ending an effort can result in missed opportunities to make Soldiers safer or more effective. To successfully make such high-stakes decisions, decision-makers must insist that information provided to them is based on appropriate data and that the information quantifies risk. Only by doing so can they make risk-aware decisions in the best interest of our Soldiers.
For more information on applying design of experiments and statistical analysis to military systems, visit: https://testscience.org/design-of-experiments.
JASON MARTIN has been the test design and analysis lead for nine years at the U.S. Army Combat Capabilities Development Command Aviation & Missile Center. He has an M.S. in statistics from Texas A&M University and an MBA and a B.S. in mechanical engineering, both from Auburn University. He is Level III certified in test and evaluation and in engineering.
Read the full article in the Fall 2020 issue of Army AL&T magazine.
Subscribe to Army AL&T News – the premier online news source for the Army Acquisition Workforce. ![]() Subscribe
Subscribe







