
By Jason Martin
Say Bert and Ernie are working together to push a heavy box on a dolly across the floor. (See Figure 1.) You want to conduct an experiment to estimate, on average, how hard each of them pushes. The dolly moves easily in all directions. You will measure how far the box moves in five seconds to determine how hard each of them is pushing. Bert and Ernie represent the variables we control in any experiment. Since neither Bert nor Ernie will push exactly the same way each time, you will ask them to do this several times to avoid making your conclusion based on an unusual data point.
FIGURE 1

OBJECT IN MOTION: If Bert and Ernie were pushing a box at the same time, how could you tell which was pushing harder? If they were on adjacent sides of the box, as shown in the middle example, it would be easy to tell how hard each one was pushing. (Graphic by USAASC)
If Bert and Ernie push on the same side of the box (in the same direction at the same spot) as shown in the right side of Figure 1, there’s no way to know how hard each one is pushing. This is a worst-case scenario, and sometimes occurs when people don’t use statistical methods to design experiments. If this happens, you can know how hard they pushed together, but there is no way to understand their individual contributions. Their effects are confounded. This is what happened in our sensor test. Because of the way the test was changed, it was as if the error and some of the other variables that we controlled were pushing from nearly the same side of the box, and it kept us from understanding how each of variable affected the result.
The middle picture shows our goal when designing an experiment. Because Bert and Ernie are on adjacent sides of the box (pushing perpendicular to each other), it is easy to tell how hard each one is pushing.
When planning or modifying an experiment, our goal is to plan it so that the variables we are controlling mimic Bert and Ernie pushing on adjacent sides of the box. This allows us to understand—accurately—how each variable we control affects the result we measure.
When we plan a test by thinking of interesting things to try, but without using appropriate statistical methods, the results are often somewhere in between the best and worst case scenarios. The effect is that we don’t understand the effects of variables as well as we could. With several variables, this can easily become a big problem.
WHAT’S THE DAMAGE?
The two mistakes in the sensor test have different consequences. First, by not knowing how much data was needed to determine whether the error improved the vehicle’s ability to avoid detection, it is possible that the test was modified unnecessarily. However, modifying the test incorrectly was the biggest mistake—it resulted in a less accurate understanding of the effect each variable had on the ability of the vehicle to avoid the sensor.
To see the consequences of incorrectly changing the test, it is useful to look at the results of data analysis. Often the most informative way to analyze data is with some kind of statistical analysis. Regression analysis of the Bert and Ernie experiment created the two plots in Figure 2.
FIGURE 2
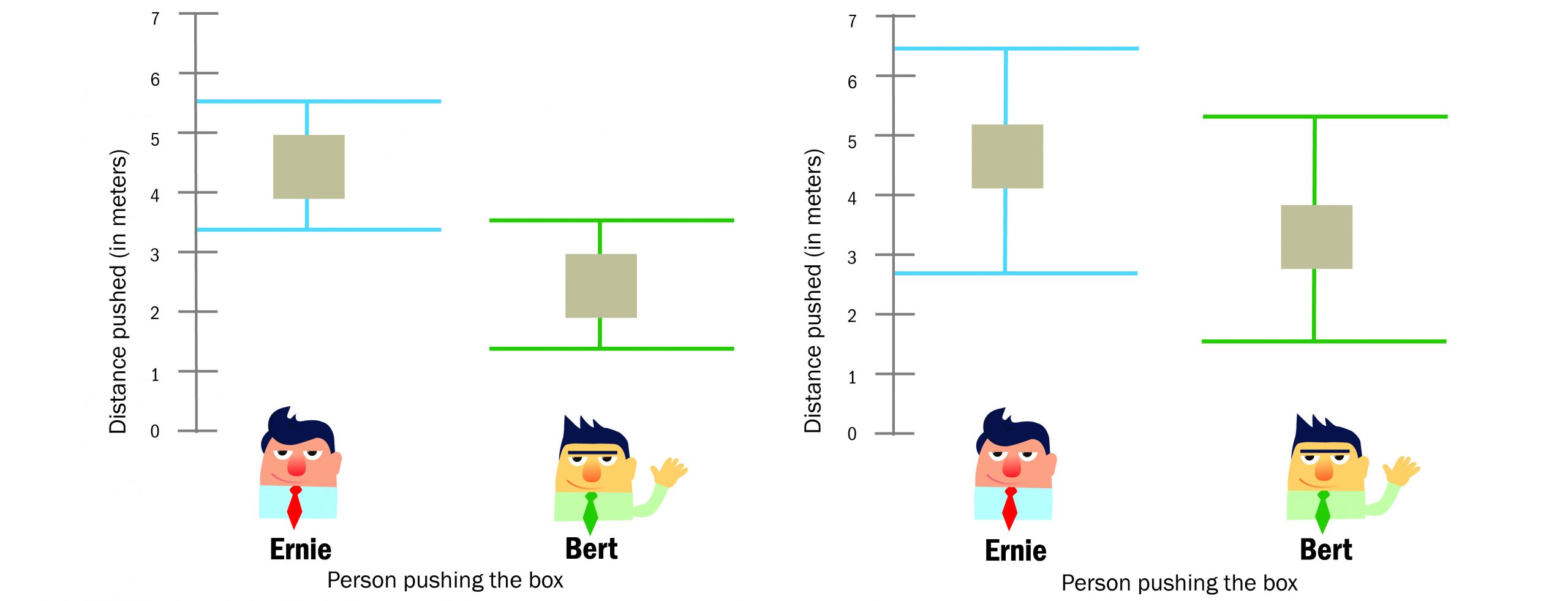
REDUCING UNCERTAINTY: The plot on the left shows the results of a well-designed experiment. In the example on the right, the two results have considerable uncertainty. While the squares are in similar places in both examples, the possible range is much larger on the right. These ranges represent the uncertainty about how far Bert and Ernie push the box on average. (Graphic by USAASC)
The plots show the results of analysis for two experiments. The plot on the left is from analysis of a well-designed experiment and on the right from a poorly designed experiment. The black dots represent the estimated or most likely value of the average distance that Bert and Ernie push the box. Notice that the black dots are in similar places on both plots, meaning that the estimated values are similar from both the good and bad experiments.
Values within the ranges of the bars are those that are reasonably believable based on the data. These ranges represent the uncertainty in our conclusions regarding how far Bert and Ernie push the box on average. Notice there is much more uncertainty in the plot on the right from the poorly designed experiment. Using the plot from the well-designed experiment on the left, we can conclude with little risk that Ernie is pushing harder than Bert.
This increase in uncertainty is a result of the ways the tests were planned. The increase is moderate compared to what can easily occur. Because of the increased uncertainty, there will be more risk involved for any decision that depends on understanding how hard each of them pushes.
In the sensor example, the way the test was modified caused uncertainty to increase so much that we could not form any meaningful conclusions about how the error or several of the other test variables affected the ability of the vehicle to avoid the sensor.
Changing the sensor test appears to have been unwarranted, and the way it was changed increased the uncertainty in our conclusions to the extent that they were not useful.
This sidebar was published to accompany the article “THE OVERSIZED POWER OF SMALL DATA” published in the Summer 2021 Issue of Army AL&T Magazine.







